Alexander Wietek | Research

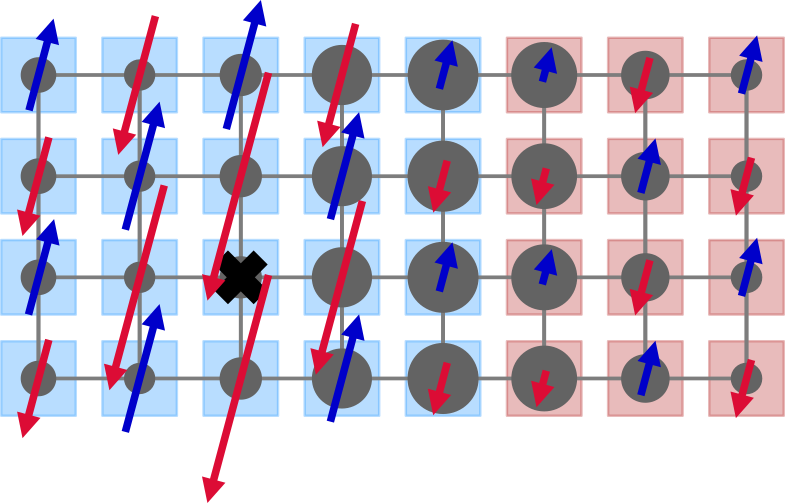
Strongly correlated electrons

To answer why matter behaves the way it does we need to understand how macroscopic physics emerges from the microscopic laws describing the motions of electrons and atoms. Naturally, things become interesting if particles interact strongly and their collective behavior is starkly different from the behavior of individual constituents. The strange laws of quantum mechanics describing electrons and atoms add some additional spice, but also complexity to this endeavor. I am studying fundamental models describing the physics of interacting electrons to understand how different states of matter emerge. This includes the stripe and pseudogap physics of the hole-doped Hubbard model at finite-temperature which I studied using a tensor network technique called METTS.

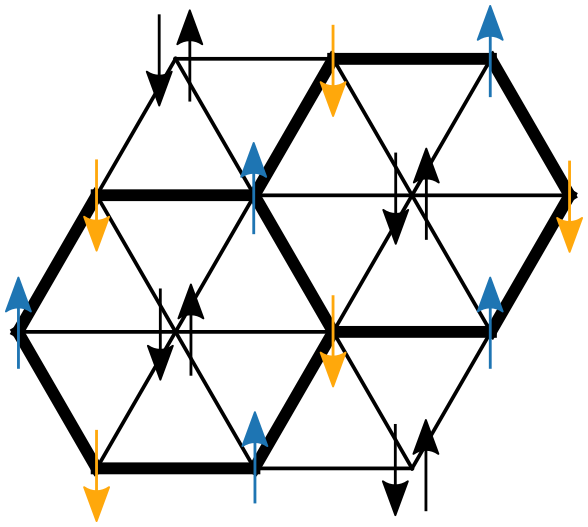
Frustrated Magnetism

Frustrated magnets are systems where local magnetic moments cannot be properly aligned at low temperatures. The resulting strong fluctuations can cause the system to stabilize exotic states of matter. This includes several (chiral) spin liquids and valence bond solids, for which I have demonstrated that they can emerge in rather simple Heisenberg antiferromagnets.

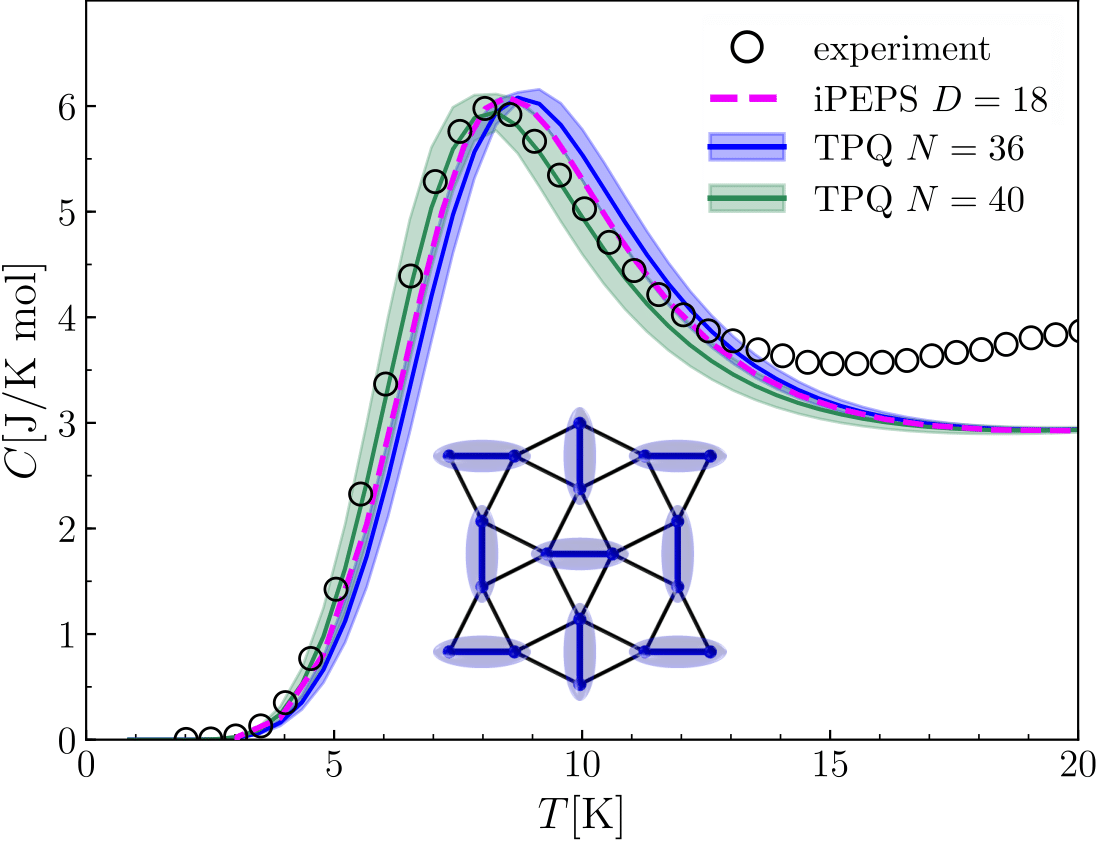
Quantum typicality methods

In quantum statistics, a thermal state in the canonical ensemble is represented by a Gibbs density matrix of the form \(\rho = \textrm{e}^{-\beta H}\). Several modern approaches replace the density matrix by a classical ensemble of pure quantum states, called thermal typical states. These reformulations turn out to be extremely useful for numerical simulations. I have employed variants of this technique to investigate several interesting problems, including the stripe and pseudogap physics of the Hubbard model and the thermodynamics of the Shastry-Sutherland model and SrCu₂(BO₃)₂, which I describe in more detail here.

High Performance Computing for quantum many-body systems

The quantum many-body problem is exponentially hard in the number of particles. For quantum spin systems the Hilbert space dimension scales as \(2^N\), where \(N\) denotes the number of spins. I have been working on high-performance computing aspects of exact diagonalization by developing novel algorithms for employing conservation laws and distributed memory parallelization. The implementation of these ideas led to the first exact ground state simulation of an \(N=50\) spin system.