Quantum typicality methods

In quantum statistics, a thermal state in the canonical ensemble is represented by a Gibbs density matrix of the form $\rho = \textrm{e}^{-\beta H}$. Several modern approaches replace the density matrix with a classical ensemble of pure quantum states, called thermal typical states. These reformulations turn out to be extremely useful for numerical simulations. I have employed variants of this technique to investigate several interesting problems, including the stripe and pseudogap physics of the Hubbard model and the thermodynamics of the Shastry-Sutherland model and SrCuBo, which I describe in more detail here.

The material SrCu₂(BO₃)₂ has been found as one of the first candidates for realizing a quantum spin liquid. Several remarkable observations have been made in this material, including a pressure-induced quantum phase transition and a fascinating series of magnetization plateaux. SrCu₂(BO₃)₂ is closely modeled by the so-called Shastry-Sutherland model of interacting spin-$1/2$ moments. While this model is paradigmatic in the field of frustrated magnetism, numerical methods have so far not been capable of simulating finite-temperature properties that could be compared to actual experimental data. 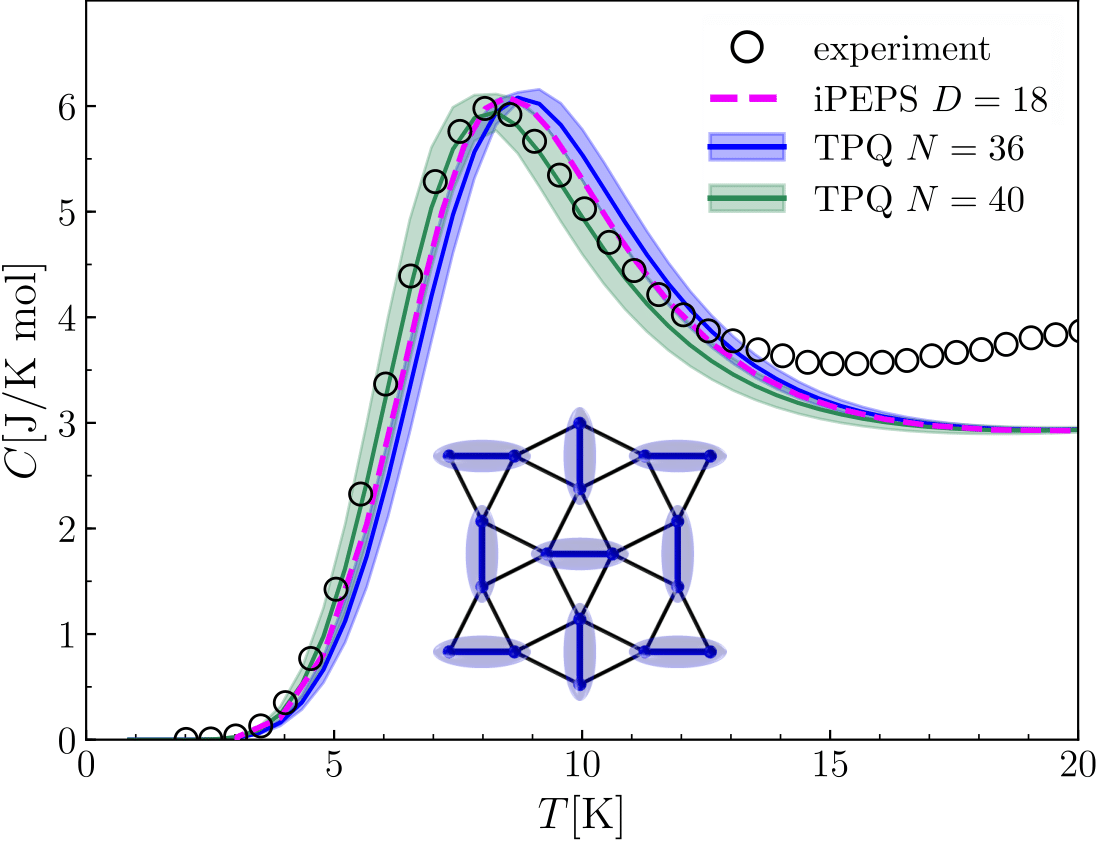In a recent paper, I have finally succeeded in simulating the thermodynamic properties of this model and validating it against experimental specific heat and susceptibility measurements. We find remarkable agreement between experiment and theory and give a detailed explanation of the peculiar behavior of these measurements. This achievement has been made possible by advancing two numerical techniques, showing convergence in their respective control parameters while arriving at consistent results.

Specific heat measurements of SrCu₂(BO₃)₂ agree with our numerical predictions from the Shastry-Sutherland model .

The technique I developed leading to successful simulations of SrCu₂(BO₃)₂ is based on the concept of thermal typical states. As a key contribution, I proposed an efficient way of combining this technique with the Lanczos approximation. I have since applied this technique also to other problems, including a recent study concerning the physics of high-temperature superconductors. While the cuprate superconductors have important technological applications, the mechanisms leading to this puzzling phenomenon remain not fully understood. While the Hubbard model of interacting electrons is believed to capture the most essential ingredients, our capabilities of simulating this model are still limited.

Here, I recently demonstrated a clear way forward by developing the so-called minimally entangled thermal typical state (METTS) method. The METTS method combines the strengths of thermal typical states with modern tensor network algorithms to simulate systems at finite temperature. Even though tensor network methods have closed in on understanding the ground state physics, finite-temperature extensions have not yet been successfully applied. This is what I have now achieved in recent work. My simulations give access to the entire temperature range from the high-temperature incoherent regime down to essentially ground state temperatures on cylindrical geometries up to sizes of $32 \times 4$. Focusing on a particular hole-doping, I establish the onset temperature of the ground state stripe phase, and discover a novel metallic phase above at higher temperatures strongly reminiscent of the pseudogap regime in cuprates.